ASR(Automatic Speech Recognition) 분야에서 모델 성능을 평가할 때 WER(Word Error Rate), CER(Character Error Rate) 같은 지표를 쓴다. Edit Distance 알고리즘을 이용해서 모델이 내놓은 결과(hypothesis)가 실제 정답과 얼마나 비슷한지 점수를 매기는 방식이다.

그런데 인식(Recognition), 분류(Classification), 탐지(Detection) 같은 다른 머신러닝 task에서는 Accuracy, Precision, Recall 같은 또 다른 지표들이 자주 등장한다. 얘네들은 이름도 비슷비슷해서 헷갈리기 딱 좋다. 특히 Precision이랑 Recall은 뭐가 다른 건지, TP, FP, FN, TN은 또 뭔지… @_@

오늘은 이 용어들의 의미를 명확히 하고, 특히 Binary Classification(이진 분류) 상황에서 얘네들을 어떻게 써먹고 해석해야 하는지, 데이터 분석가의 마음(?)으로 한번 정리해보려 한다.

혼동 행렬 (Confusion Matrix): 모든 것은 여기서 시작된다

분류 모델의 성능을 이야기할 때 빼놓을 수 없는 것이 바로 Confusion Matrix(혼동 행렬)이다. 이름 한번 거창하지만, 알고 보면 그냥 모델의 예측 결과랑 실제 정답을 표로 정리한 거다. 이 표 하나로 모델이 뭘 잘하고 뭘 못하는지 한눈에 파악할 수 있다.

Binary Classification에서는 보통 Positive(긍정, 1) / Negative(부정, 0) 두 클래스로 나눈다. 예를 들어 ‘스팸 메일 분류’라면 스팸 메일이 Positive, 정상 메일이 Negative가 될 수 있다. 이걸 기준으로 혼동 행렬은 다음과 같이 4가지 경우의 수를 보여준다.

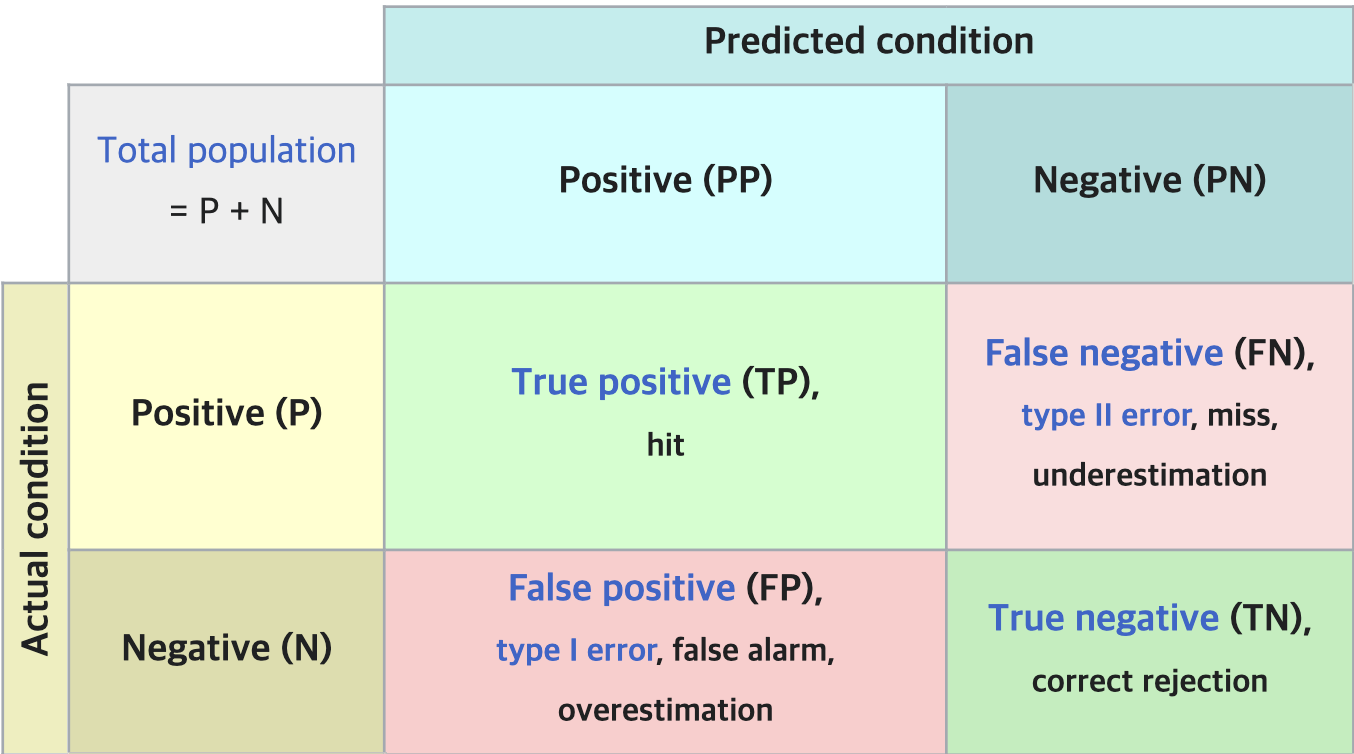
Confusion Matrix 예시

  • TP (True Positive): 실제 Positive인 것을 Positive라고 정확히 예측한 경우. (정답!) - “이건 스팸이야!” 라고 했는데 진짜 스팸.
  • TN (True Negative): 실제 Negative인 것을 Negative라고 정확히 예측한 경우. (정답!) - “이건 스팸 아니야!” 라고 했는데 진짜 정상 메일.
  • FP (False Positive): 실제 Negative인 것을 Positive라고 잘못 예측한 경우. (1종 오류, Type I Error) - “이건 스팸이야!” 라고 했는데… 억울한 정상 메일.
  • FN (False Negative): 실제 Positive인 것을 Negative라고 잘못 예측한 경우. (2종 오류, Type II Error) - “이건 스팸 아니야!” 라고 했는데… 놓쳐버린 스팸.

이 네 가지 값(TP, TN, FP, FN)만 알면 지금부터 설명할 모든 지표를 계산할 수 있다. 그야말로 분류 모델 성능 평가의 알파이자 오메가!

Accuracy (정확도): 가장 직관적, 하지만 함정이?

자, 이제 본격적으로 성능 지표들을 살펴보자. 가장 먼저 만나볼 친구는 Accuracy(정확도)다.

$$ ACCURACY = \frac{TP+TN}{TP + TN + FP + FN} = \frac{맞춘 것}{전체} $$

수식을 보면 알겠지만, 그냥 전체 예측 건수 중에서 정답을 맞춘 비율이다. TP와 TN을 더해서 전체(TP+TN+FP+FN)로 나눈 값. 100문제 중에 90문제 맞히면 정확도 90%인 것처럼 아주 직관적이다. 뭔가 시험 성적표 받는 느낌이랄까?

Accuracy = (잘 맞춘 스팸 개수 + 잘 맞춘 정상 메일 개수) / (전체 메일 개수)

여기까지만 보면 Accuracy가 무난하고 괜찮아 보인다. 높으면 무조건 좋은 모델 아닌가? 하지만 세상은 그렇게 단순하지 않다. Accuracy에는 치명적인 단점이 숨어있다. 바로 데이터가 불균형(imbalanced)할 때 성능을 제대로 반영하지 못한다는 점이다.

예를 들어, 1000개의 메일 중 스팸 메일(Positive)이 단 10개뿐이고 나머지 990개가 정상 메일(Negative)인 데이터셋이 있다고 치자. 이때 모델이 모든 메일을 그냥 “정상 메일이야!"(Negative)라고 예측해버리면 어떻게 될까?

  • TP = 0 (스팸을 스팸이라 예측 못함)
  • TN = 990 (정상 메일을 정상이라 예측함)
  • FP = 0 (정상 메일을 스팸이라 예측 안함)
  • FN = 10 (스팸을 정상이라 예측함)

이 모델의 Accuracy를 계산해보면?

$$ Accuracy = \frac{0 + 990}{0 + 990 + 0 + 10} = \frac{990}{1000} = 99% $$

무려 99%의 정확도! 와, 엄청난 모델이다..! 최강의 모델인가 보다! 라고 생각하면 큰일 난다. 이 모델은 스팸 메일을 단 하나도 걸러내지 못하는, 사실상 쓸모없는 모델이다.

이처럼 데이터 클래스 비율이 한쪽으로 크게 치우쳐 있으면, 다수 클래스만 잘 맞춰도 Accuracy는 높게 나올 수 있다. 그래서 Accuracy만 보고 모델 성능을 판단하는 것은 매우 위험하다.

Precision (정밀도) & Recall (재현율): Accuracy의 빈틈을 메우다

Accuracy의 함정을 피하기 위해 등장한 구원투수들이 바로 Precision(정밀도)과 Recall(재현율)이다. 이 둘은 모델의 예측 결과를 좀 더 다른 관점에서 바라본다.

Precision (정밀도): “내가 Positive라고 한 것 중에 진짜는?”

$$ PRECISION = \frac{TP}{TP + FP} = \frac{진짜 Positive}{Positive라고 예측한 것들} $$

Precision은 모델이 Positive라고 예측한 것들 중에서, 실제로 Positive인 것의 비율이다. 즉, 모델의 Positive 예측이 얼마나 정확한지를 나타낸다.

Precision = (잘 맞춘 스팸 개수) / (모델이 스팸이라고 예측한 전체 메일 개수)

Precision이 높다는 것은 모델이 “이건 Positive야!“라고 했을 때, 그 예측을 믿을 만하다는 뜻이다. 스팸 메일 분류 예시에서는, 모델이 스팸이라고 분류한 메일들 중 실제 스팸일 확률이 높다는 의미다. FP(정상 메일을 스팸으로 잘못 예측)가 낮을수록 Precision은 높아진다. 괜히 억울하게 스팸함으로 가는 정상 메일을 줄이고 싶을 때 중요한 지표다.

Recall (재현율): “실제 Positive 중에 내가 얼마나 찾아냈지?”

$$ RECALL = \frac{TP}{TP + FN} = \frac{진짜 Positive}{실제 Positive인 것들} $$

Recall은 실제 Positive인 것들 중에서, 모델이 Positive라고 예측한 것의 비율이다. 즉, 모델이 실제 Positive 샘플을 얼마나 놓치지 않고 잘 찾아내는 지를 나타낸다. Sensitivity(민감도)라고도 불린다.

Recall = (잘 맞춘 스팸 개수) / (실제 스팸 메일 전체 개수)

Recall이 높다는 것은 모델이 실제 Positive 샘플들을 놓치지 않고 잘 잡아낸다는 뜻이다. 스팸 메일 분류 예시에서는, 실제 스팸 메일들을 빠짐없이 잘 걸러내는 능력을 의미한다. FN(스팸을 정상 메일로 잘못 예측)이 낮을수록 Recall은 높아진다. 단 하나의 스팸 메일도 놓치고 싶지 않을 때 중요한 지표다.

그래서 뭘 써야 하냐고? Task 나름!

Accuracy가 항상 능사는 아니라는 것, Precision과 Recall의 계산법과 의미가 다르다는 것은 이제 알겠다. 그래서 어쩌라는 건가..? 어디서 주워듣기로 통계는 해석의 학문이라고 한다. 여기서도 비슷하다. 어떤 지표를 중요하게 볼지는 풀고자 하는 문제(Task)의 특성에 따라 달라진다. 왜냐하면 FP와 FN 중 어떤 실수가 더 치명적인가가 Task마다 다르기 때문이다.

다시 한번 두 가지 Task를 예로 들어보자.

  1. 스팸 메일 필터링:

    • FP (정상 메일을 스팸으로): 중요한 메일을 놓칠 수 있다. (짜증 유발)
    • FN (스팸 메일을 정상으로): 귀찮은 스팸 메일을 받게 된다. (귀찮음 유발)
    • 상대적으로 FP가 더 치명적일 수 있다. 중요한 메일을 놓치는 것보다는 스팸 몇 개 더 받는 게 나을 수도? 이 경우 Precision이 중요해진다.

  2. 암 진단 모델:

    • FP (정상인을 암 환자로): 환자는 불필요한 검사와 스트레스를 받는다. (비용, 심리적 부담)
    • FN (암 환자를 정상인으로): 치료 시기를 놓쳐 생명이 위험해질 수 있다! (매우 치명적!)
    • 이 경우, FN을 줄이는 것이 압도적으로 중요하다. 즉, 실제 암 환자를 한 명이라도 놓치지 않아야 하므로 Recall이 매우 중요해진다. 차라리 정상인을 암 환자로 오진(FP)하더라도, 실제 환자를 놓치는(FN) 것보다는 낫다고 판단할 수 있다.

이처럼 Task의 맥락에서 어떤 오류(FP or FN)를 더 피하고 싶은지에 따라 Precision과 Recall의 중요도가 달라진다. 모델을 평가할 때는 내가 풀려는 문제가 무엇인지, 어떤 실수가 더 큰 문제를 일으키는지 먼저 고민해야 한다. 데이터가 주어졌을 때, 이 상황을 잘 분석해서 어떤 지표를 중점적으로 볼지 결정하는 것이 중요하다.

F1-Score: Precision과 Recall, 둘 다 놓치지 않을 거예요!

“아니, Precision이랑 Recall 둘 다 중요하면 어떡하라고? 하나만 고르기 너무 어려운데?” 라는 생각이 들 수 있다. 실제로 많은 경우 Precision과 Recall은 서로 반비례(Trade-off) 관계에 있다. 하나를 높이려고 하면 다른 하나가 낮아지는 경향이 있다. (모델의 예측 임계값(threshold)을 조정해보면 이 관계를 확인할 수 있다.)

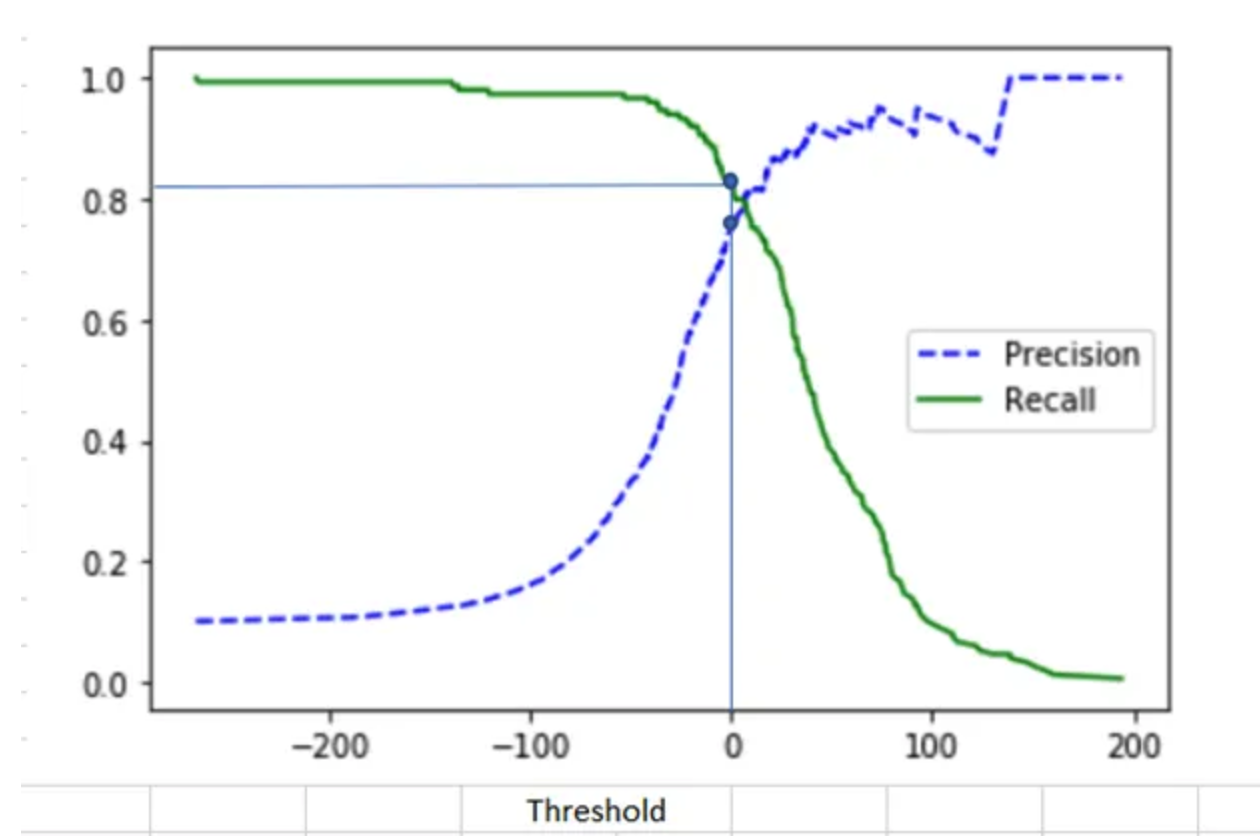
trade off in precision and recall

그래서 등장한 것이 F1-Score다. F1-Score는 Precision과 Recall의 조화 평균(Harmonic Mean)을 계산하여, 두 지표를 균형 있게 고려하려는 지표다.

$$ F1 = 2 \times \frac{PRECISION \times RECALL}{PRECISION + RECALL} $$

왜 그냥 산술 평균((Precision + Recall) / 2)이 아니라 조화 평균을 쓸까? 조화 평균은 두 값 중 낮은 쪽에 더 큰 가중치를 주는 특징이 있다. 따라서 Precision과 Recall 어느 한쪽이라도 값이 매우 낮으면, F1-Score 역시 낮게 나온다. 즉, F1-Score가 높다는 것은 Precision과 Recall이 모두 어느 정도 높은 수준을 유지하고 있다는 의미로 해석할 수 있다. 둘 중 하나만 극단적으로 높고 다른 하나는 매우 낮은 경우, F1-Score는 낮게 평가하여 불균형을 잡아준다.

F1-Score는 특히 클래스 불균형이 심하거나, Precision과 Recall 모두 중요한 Task에서 유용하게 사용된다.

(참고: F-measure는 F1-Score를 일반화한 것으로, β 값을 조절하여 Precision 또는 Recall에 더 가중치를 줄 수 있다. F1-Score는 β=1인 경우로, Precision과 Recall을 동일한 비중으로 고려한다.)

결론: 상황에 맞는 지표 선택과 종합적인 판단이 핵심

정리해보자.

  • Accuracy: 가장 직관적이지만, 데이터 불균형에 취약하다.
  • Precision: Positive 예측의 정확성. FP를 줄이는 것이 중요할 때. (예: 스팸 필터)
  • Recall: 실제 Positive를 놓치지 않는 능력. FN을 줄이는 것이 중요할 때. (예: 암 진단)
  • F1-Score: Precision과 Recall의 조화 평균. 둘 다 중요할 때 균형 있게 평가.

어떤 지표가 절대적으로 좋다고 말할 수는 없다. 가장 중요한 것은 Task의 특성과 목적을 이해하고, 어떤 종류의 오류가 더 치명적인지 판단하여 적절한 평가지표를 선택하거나 여러 지표를 종합적으로 고려하는 것이다. 모델의 성능 숫자에만 매몰되지 말고, 그 숫자가 실제 상황에서 어떤 의미를 가지는지 해석하는 능력이 중요하다 하겠다.

References