leet code WC439에 나온 palindrome 문제이다. 주요 포인트는 2가지로 말할 수 있다.
- subsquence 문제는 DP 방법을 떠올려 볼 것.
- 만약 DP로 접근하기로 결정하고, 2차원 배열을 두고 DP문제로 가정했을 때, bottom-up 방식이라면 2차원 배열 DP에서는 먼저 아래 그림과 같이 생각할 줄 알아야 한다.
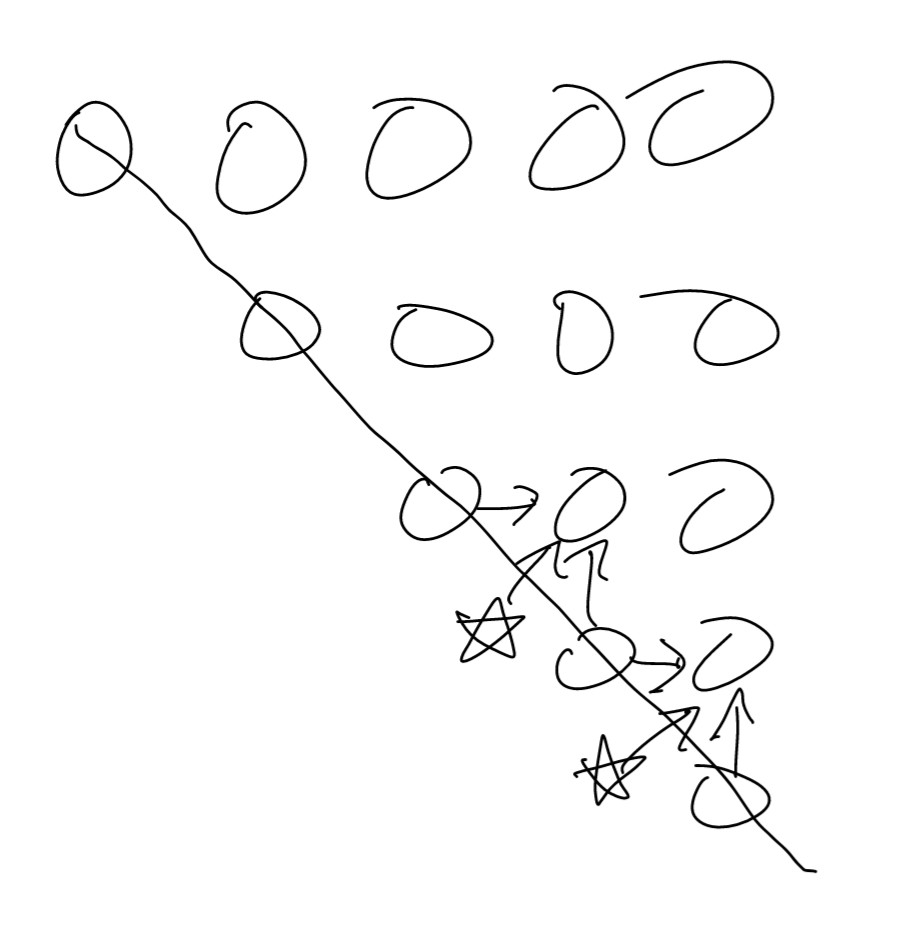
위 2가지 포인트를 가지고 있다면 좀 더 쉽게 문제를 풀 수 있을 것이다.
class Solution:
def longestPalindromicSubsequence(self, s: str, k: int) -> int:
def cost(c1, c2):
dist = abs(ord(c1) - ord(c2))
return min(dist, 26-dist)
# k + 1 because we store 0 to k
n = len(s)
dp = [[[0 for _ in range(k+1)] for _ in range(n)] for _ in range(n)]
for i in range(n):
for kk in range(k+1):
# single character is palindrome
dp[i][i][kk] = 1
for i in range(n-1, -1, -1):
for j in range(i+1, n):
# print("i, j", i, j)
for kk in range(k+1):
if s[i] == s[j]:
dp[i][j][kk] = dp[i+1][j-1][kk] + 2
else:
dp[i][j][kk] = max(dp[i+1][j][kk], dp[i][j-1][kk])
d = cost(s[i], s[j])
if d <= kk:
dp[i][j][kk] = max(dp[i][j][kk], dp[i+1][j-1][kk-d] + 2)
return dp[0][n-1][k]


...